on the occasion of the General Elections of November 10, Angelica Benito Sualdea and Adolfo Quirós Gracián, professors of Mathematics at the Autonomous University of Madrid, we present a new electoral challenge proposed by THE COUNTRY and the Royal Mathematical Society of Spain. On this occasion try to see how it affects the method of allocation to the proportional allocation of seats and, in particular, whether a party may or may not lose seats “whole”. Readers can send their answers to 00.00 Saturday, November 9 (midnight of Friday to Saturday, gmt) to problemamatematicas@gmail.com. Then, to clarify, we add the statement of the problem in writing.
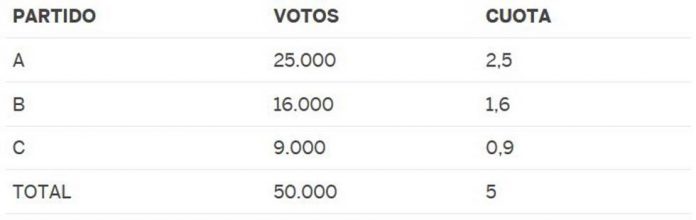
The Spanish Constitution prescribes that in elections to Congress of Deputies, the allocation of seats to the parties should be done in each constituency, with criteria proportional. In principle this is not required but a rule of three: if there is a deal And seats, have voted P people and p of them have opted for a party, the amount of seats that corresponds to that match (that is called your share) will be q= E x p /Q. The problem is that, as we see in the following example with 3 parties, to 50,000 voters and 5 seats, so that it is easy to calculate the fees, these are not always integers:
Allocating the seats whole, correspond 2 to party A and 1 to B, but, as it is not possible to send 0,6 members of one party to the Congress, you have to decide to whom to attribute the 2 remaining seats. One way to do this is to give the parties whose fees have decimal part bigger, in this example C and B, so that the distribution would be like this:
This procedure is known as the Method of Largest Remainders, and is in fact what our Electoral Law says to be done to establish how many seats are elected in each province. But to distribute seats between parties within a constituency, the Electoral Law says that you must use the Method D’hondt, whose operation we remember: divide the votes of the parties between 1, 2, 3,… and the seats are assigned successively to the parties with the highest quotients. In our example (we note in bold the ratios that obtained seats) the result would be:
MORE INFORMATION
See more challenges mathematicians
we do Not want to discuss if this division is more or less proportional than the previous one, because our goal is another: observe that, although it might seem that with the Method of D’hondt, the party has “taken” a seat at the B in reality the loss of B with respect to its share is only 0.6 seats, and keeps the seat a whole that was due him. It is not difficult to demonstrate that the Method D’hondt always true this property: it assigns to all parties, and in any situation, at least the integer part of its quota. It can not therefore be said, as is sometimes heard, that “D’hondt remove seats to the smaller parties to give to the great.” The slight premium that they can get the big parties in a given constituency comes solely from the allocation of parts decimal of seats, no of seats integers. (Another thing is the advantage to the big parties that the elections to the Congress are actually 52 separate elections, one for a constituency, sharing in the majority of them very few seats).
But there are other methods to allocate seats more or less proportionately. For example, the Sainte-Laguë, which has been proposed as a possible alternative for the elections to the Congress of Deputies. Its operation is similar to D’hondt, except that now the votes are divided only between the odd numbers. This would be the result of applying it to our example:
As you see, the party B retrieves the seat that had been “lost” with D’hondt. It is perhaps surprising that not all methods of sharing to share with D’hondt the natural property that, in any situation, no party to lose seats “whole”. In particular, the Method of Sainte-Laguë can in some cases (not the case in our example) to assign to a party less seats of which indicates the integer part of its quota.
The challenge that we propose to our readers is that we submit an example in this situation: there is a party to which the Method of Sainte-Laguë does not assign all seats integers which corresponded according to their fee .
those Who dare are free to choose the number of seats to be divided, the parties, the total of voters, and how many decide to vote for each party.
we Hope that you also give a brief indication of how they have arrived at the example. we look forward to your replies.